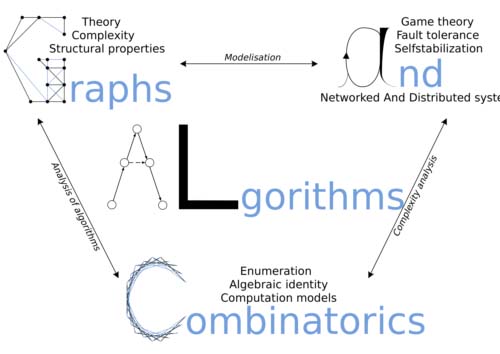
Graphs, Algorithms and Combinatorics (GALaC)

The main goal of this group is to design, model, study the control and performance of algorithms designed specifically for distributed systems and their applications. The scientific contribution we aim at is both theoretical with the development of new mathematical models and quality proofs and also applied with the development of innovative tools for different types of networks (opportunistic, content-centric or congitive).

More precisely, the objectives of the ANS group (for Algorithms for Networked systems) are:

• To establish basic building blocks for the design and optimization of networked systems. This includes control theory, game theory, distributed algorithms and especially self-stabilization and fault tolerance as well as simulation of systems via discrete event models.
• To design efficient algorithms and protocols based on the development of theoretical frameworks, and to evaluate their performance through practical scenarios. This includes opportunistic wireless networks (e.g., robot networks, ad hoc wireless networks, sensor networks), future infrastructure and protocols for the Internet (information, content-centric networks), security and safety in cyber-physical systems.

The collaborations of this axis take place on the 5 continents.

The main interest of this activity is the study of the relationship between algebraic structures and algorithms. The researchers are particularly interested in the following topics:

• Algebraic structures (combinatorics of Hopf algebras, Operads, Monoids, ...) related to algorithms;
• Enumerative combinatorics and symbolic dynamics.
• Object-oriented software designed for mathematical modeling, in particular the development of the SageMath software;

More precisely, the research projects are related to algebraic combinatorics, are at the interface of enumerative combinatorics and concern the analysis of algorithms from the point of view of symbolic and algebraic computations. The objectives are twofold: first, thanks to a massive generalization of the notion of generating series we hope to propose a theoretical framework allowing the study of the fine behavior of many different algorithms and second, and in a reciprocal way, the study of the same algorithms opens up new avenues for the discovery of objects or algebraic identities of interest. These identities have several applications in mathematics, in particular in representation theory but also in physics (mainly in statistical physics).

The research is largely based on computer experimentation, with a significant amount of development via the Sage-Combinat software project.

However, the level of sophistication, flexibility and quality of the required computational tools has reached a point where, on a large scale, collaborative development is essential. The design and collaborative development of such software raises the search for quality. The challenges are both in the domain of computer science and around the mathematical modeling and management of a large hierarchy of (object-oriented) classes, etc.

These specific questions also raise more general combinatorial questions. It is then envisaged to work on enumerative combinatorics, cellular automata and in particular trees.

This axis feeds regular collaborations in France but also with Germany, North America and India.

The main focus is on structural and algorithmic issues. The team has established an expertise including problems such as finding large cycles of a given graph, coloring a graph, solving covering problems, or advancing graph theory by finding extreme graphs satisfying a constraint.

The generalization of some problems is also considered for edge or colored vertex graphs. For example, colored covering graphs have been studied for colored edge or vertex graphs. Alternatively it has been searched the dominant set in a graph having at least one vertex of each color. Beyond the purely theoretical interest these approaches have a great interest in the field of bioinformatics as well as in that of the Web.

Many of the questions we consider can also be stated in terms of linear optimization. This opens perspectives.

We have many collaborations with French groups: LaBRILaboratoire Bordelais de Recherche en Informatique, LIRMMLaboratoire d'Informatique, de Robotique et de Microélectronique de Montpellier, LIAFALaboratory of Algorithmic Computing: Foundations and Applications and LIMOSLaboratory of Computing, Modeling and Optimization of Systems as well as in Europe, in North and South America and mainly in Asia with China, Japan, India