LAPLACE – Learning poorly known and observed large scale systems

Title : LAPLACE – Learning poorly known and observed large scale systems

Team and research environment

The work will take place at the Laboratoire Interdisciplinaire des Sciences du Numérique on the campus of Université Paris-Saclay, benefiting from expertise of the research team in machine learning, applied mathematics, computer science, statistical physics, fluid mechanics and dynamical systems.

The candidate should ideally have a solid background in machine learning, applied maths and/or
statistics. Knowledge in machine learning numerical framework (for instance, Pytorch) is a plus.

Contacts

Lionel Mathelin (lionel.mathelin@cnrs.fr) , Onofrio Semeraro (onofrio.semeraro@cnrs.fr)

Scientific context

“Governing is forecasting”. This proverbial saying is relevant to many situations of engineering
interest where decisions must be taken based on predictions or when devising a suitable sequence of
actions to achieve some goal requires a good knowledge of the effect of these actions onto the system
under consideration. Such predictions usually rely on a simulation of a model of the system at hand
and/or observations collected over time. A reliable model may however not be available, or be too
computationally costly to be useful.

In this internship, we aim at deriving a well grounded approach to predict quantities of interest
or (approximation of) the state of a system. We will rely on the Mori-Zwanzig framework developed in
the statistical physics community in the late 60s. It formalizes the time-evolution of a set of variables
related to the system as a function of their history, without requiring knowledge of the other variables
describing the system. Accounting for the past essentially allows to isolate the dynamics of these
observables. This framework is general and applies widely. For instance, when the state of the system
is not accessible, the dynamics of the observables can be described with a non-Markovian model via
this framework. It similarly provides a principled closure for coarse models which can be effectively
complemented with a history-based term.

Relying on the past to compensate for the lack of information from the current state is a common
approach in partially observed systems where the available observations are not sufficient statistics to
predict the future evolution in a deterministic manner. One then reverts to predicting an uncertain
future, in the form of a probability distribution as is done with Kalman filters, or to account for the
past measurements to narrow down the possible futures consistent with the observations to a unique
one. The problem hence formulates as a time series prediction and has received considerable attention
owing to its ubiquity in many scientific fields, ranging from finance to climatology or biology to name a
few. State-of-the-art methods for time series prediction involve auto-regressive models, e.g., ARMAX
[5], recurrent neural networks such as LSTMLong short-term memory, echo state networks, augmented models [3] or the more
recently introduced Transformers [9] and CD-ROM approach, [7]. While often effective, these techniques
lack expressivity (ARMAX) or interpretability (recurrent networks, Transformers).

In this internship, we will explore the potential of Signatures to efficiently approximate the
history integral of the observations, [8]. The Signature transform introduced in [2, 6, 1] has recently been
used in several areas, including rough path theory, finance, stochastic control, and machine learning.
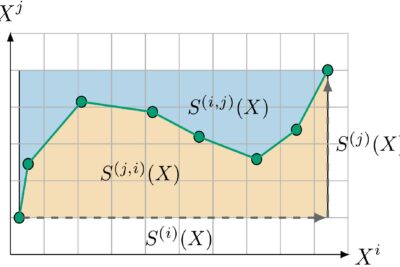
It has proven to be an effective tool to summarize the information of paths and dependencies across different dimensions, with high computational efficiency. Signatures consist of iterated integrals of the
history of its inputs and enjoys interpretability, see Fig. 1 for a sketch. They provide a way to linearize
all possible functions of their input and exhibit nice theoretical properties. In particular, owing to tensor
algebra, they can be efficiently updated when new observations become available, without recomputing
the whole object.

Research challenges

We believe Signature transforms are key enablers for a principled and efficient modeling of the
impact of past observations onto their current dynamics in a non-Markovian context. Many open
questions however remain and will be the focus of this internship. In particular, how are the different
time scales of the physical system preserved across the Signature of its observations? What are the
properties of the time series to retain in order to allow for a reliable and efficient prediction based
on Signatures? How large should the truncation order be for a given performance? How frugal can
the Signature-based term in the Mori-Zwanzig framework be in terms of training data, a critical point
in many situations? Does the Mori-Zwanzig solution has a structure that can be exploited, such as
low rankness, sparsity or multi-dependence which can be captured with tensor formats, etc.? These
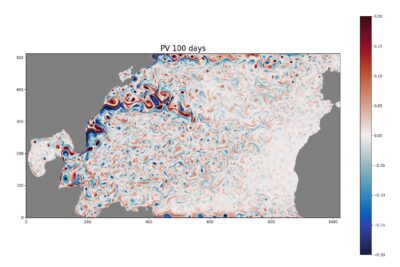
methodological developments will first be illustrated on low-dimensional dynamical systems before, if
time allows, being demonstrated on large scale real data from geophysics, see Fig. 2.

References

[1] Bonnier P., Kidger P., Arribas I. P´erez, Salvi C. & Lyons T. J., Deep Signatures, arXiv 1905.08494 , 2019.
[2] Chen K.-T., Integration of paths, geometric invariants and a generalized Baker-Hausdorff formula, Annals of Mathematics.
2nd ser., 65, p. 163–178, 1957.
[3] Dupont E., Doucet A. & Teh Y. W., Augmented Neural ODEs, In Advances in Neural Information Processing
Systems, , vol. 32, 2019.
[4] Fermanian A., Learning time-dependent data with the signature transform, Theses, Sorbonne Universit´e, 2021.
[5] Guidorzi R., Multivariable system identification: from observations to models, Bononia University Press, 2003.
[6] Lyons T., Caruana M. & L´evy T., Differential equations driven by rough paths, In Lecture notes in Mathematics,
´ Ecole d’´et´e de probabilit´es de Saint-Flour XXXIV-2004, 2007.
[7] Menier E., Bucci M.A., Yagoubi M., Mathelin L. & Schoenauer M., CD-ROM: Complemented Deep – Reduced
Order Model, Computer Methods in Applied Mechanics and Engineering, 410, p. 115985, also available on arXiv:
https://arxiv.org/abs/2202.10746, 2023.
[8] Pradeleix E., Hosseinkhan-Boucher R., Shilova A., Semeraro O. & Mathelin L., Learning non-Markovian
Dynamical Systems with Signature-based Encoders, arXiv 2509.12022 , 2025.
[9] Vaswani A., Shazeer N., Parmar N., Uszkoreit J., Jones L., Gomez A., Kaiser L. & Polosukhin I., Attention
is All you Need, In Advances in Neural Information Processing Systems, , vol. 30, 2017.